概要
機械学習の手法であるK-means法(k-means clustering, K平均法)を使って数値データの異常検知ができないかAmazon SageMakerのビルトインアルゴリズムを使って検証しました。
主に次の2点の観点から検証を行いました。興味があれば一読ください。
- 正常データのみでの学習は可能か
- shingling処理はK-means法でも有効か
K-means法とは
K-means法は、非階層的なクラスタリング手法の一つです。
この手法は、与えられたデータを事前に決められたクラスタ数K個のグループに分割するために使用されます。K-means法は、各クラスタの重心(centroid)を計算し、各データを最も近い重心に割り当てることで動作します。
K-means法のアルゴリズムは以下の通りです。
1.各データポイントを、最も近いセントロイドに割り当てる。
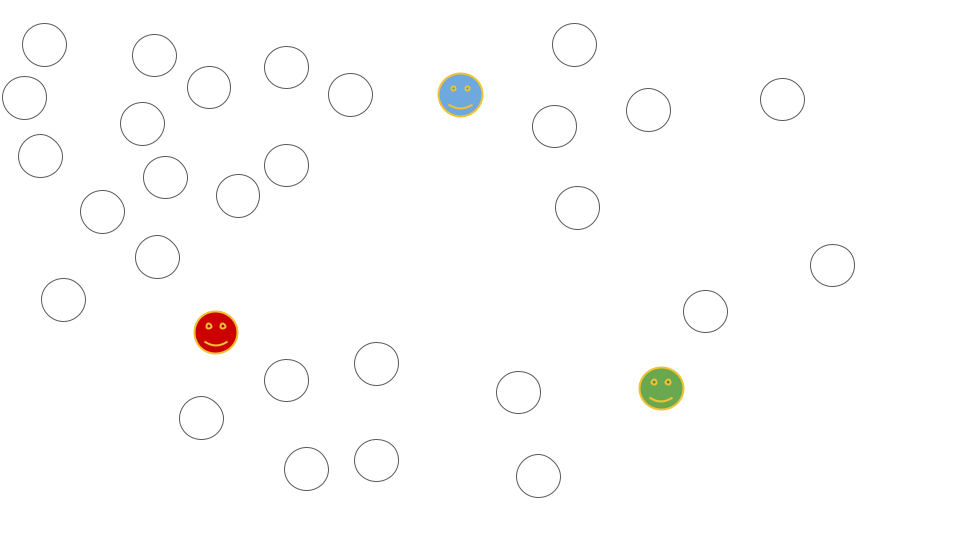
2.データセットから、K個の初期セントロイド(centroids)をランダムに選択する。
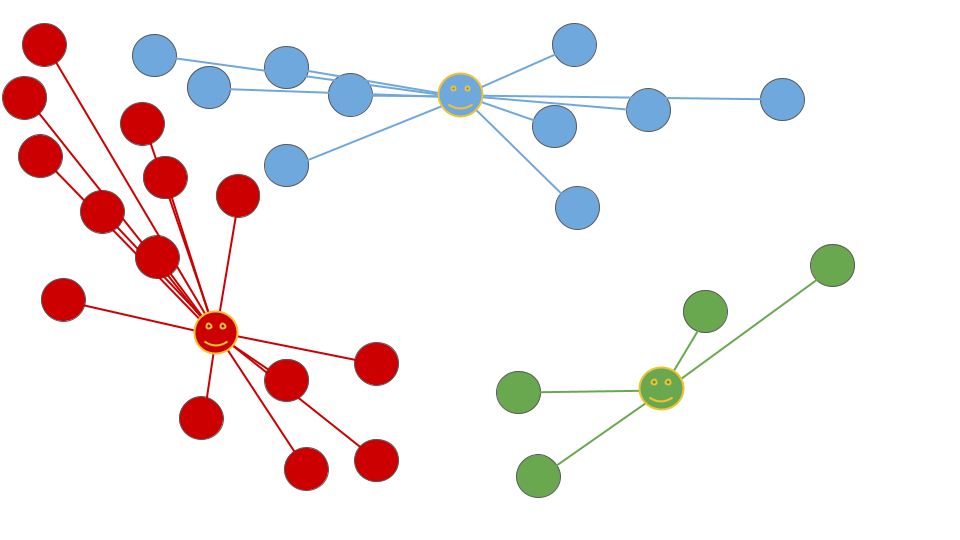
3.各クラスタに属するデータポイントの平均を計算し、その平均を新しいセントロイドとする。
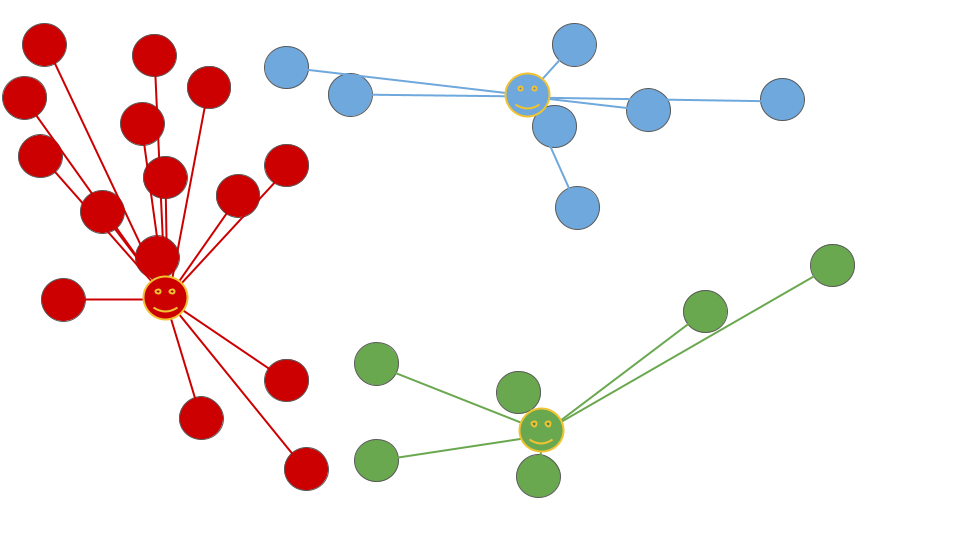
4.収束するまで、ステップ2とステップ3を繰り返す。
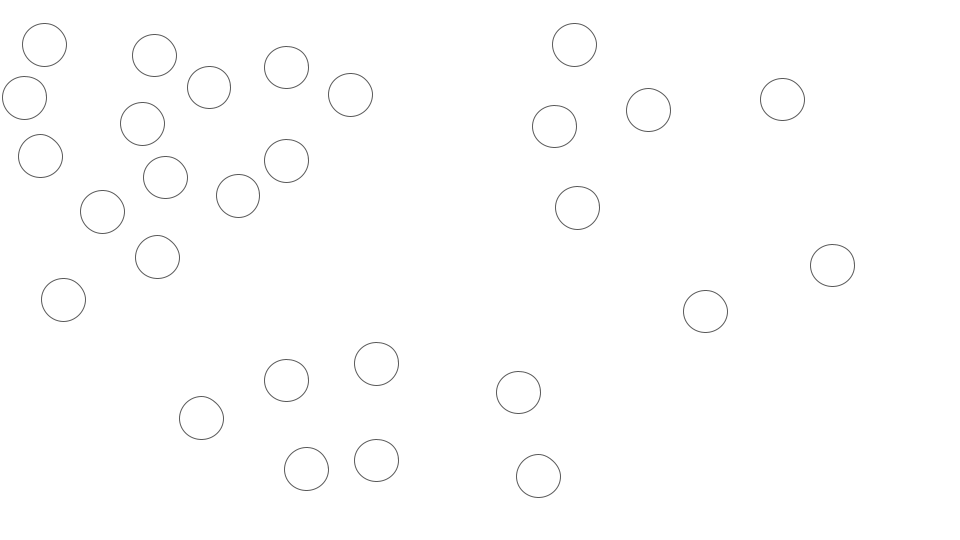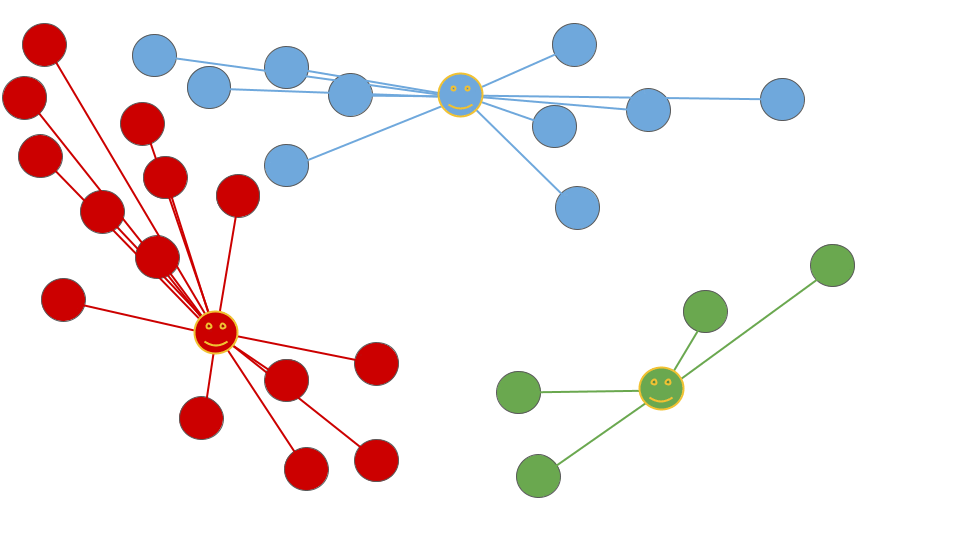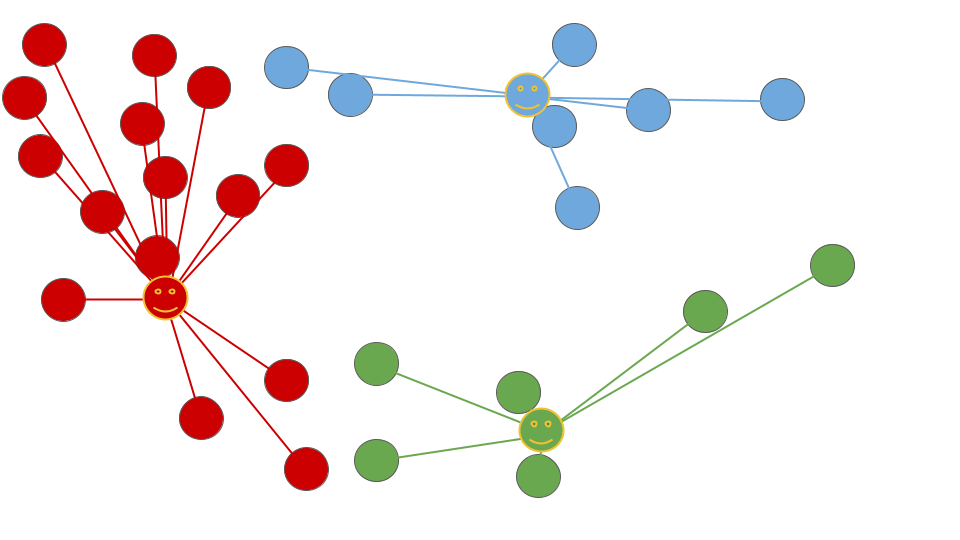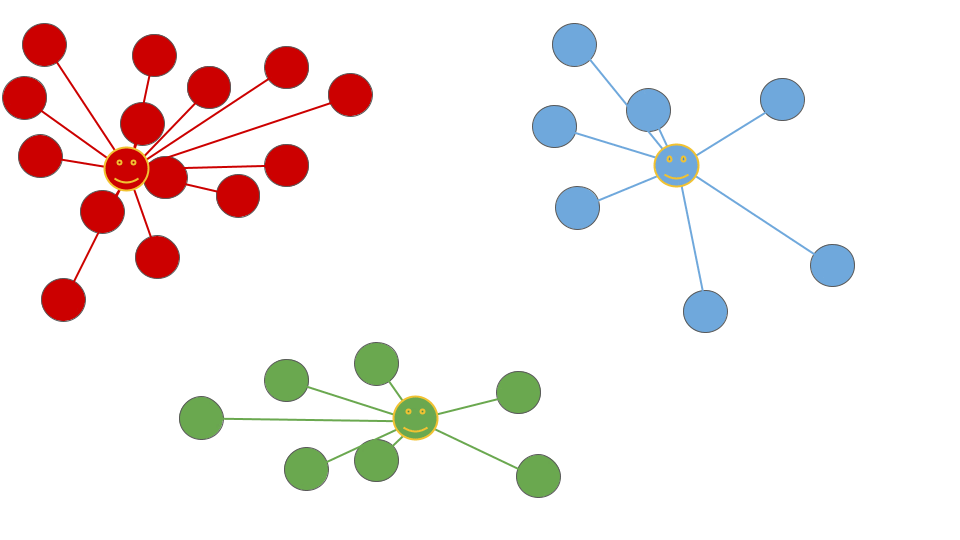
収束の条件は、クラスターが変化しなくなることです。つまり、各データポイントが最も近いセントロイドに割り当てられ、セントロイドが更新されなくなった場合、アルゴリズムは収束します。
AWSにおけるK-meansアルゴリズム
https://docs.aws.amazon.com/sagemaker/latest/dg/k-means.html
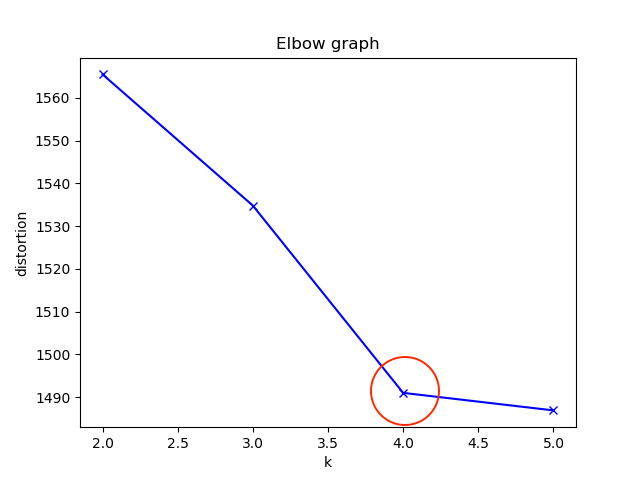
エルボー法による最適なK
エルボー法は、K-means法で使用されるクラスタ数Kを決定するための手法の一つです。
エルボー法では、クラスタ数を変化させた場合のクラスタ内誤差平方和(SSE)をプロットし、SSEの変化がエルボー(肘)のように曲がる点をKの値として選択します
エルボー法のアルゴリズムは以下の通りです。
- クラスタ数Kの値を設定する。
- K-means法を使用して、各クラスタのセントロイドと各データポイントのクラスタ割り当てを決定する。
- 各データポイントとそのクラスタのセントロイドとの距離を計算し、SSEを計算する。
- ステップ2からステップ3までを繰り返し、K個の異なるクラスタ数でSSEを計算する。
- SSEの値をプロットし、グラフを視覚的に分析する。
- SSEの変化がエルボーのように曲がる点をKの値として選択する。
数値データの異常検知
ここからはいくつかのパターンの数値データを実際にK-meansで異常分析が可能か検証してみました。
パターンとしては
- 正規乱数
- 比例データ
- 周期データ
- 実際の温度データ
で検証しています。
実際の温度データ以外は作成したデータを使って学習とテストを行なっています。
今回は各値が最も近いKからの距離を異常スコアとして扱っています。
正規乱数
正規乱数の値の中にランダムに値をスパイクさせた学習データを使用しています。
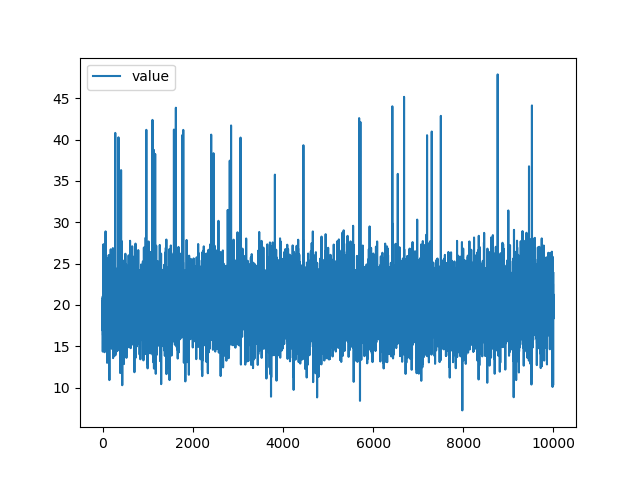
| 学習データ |
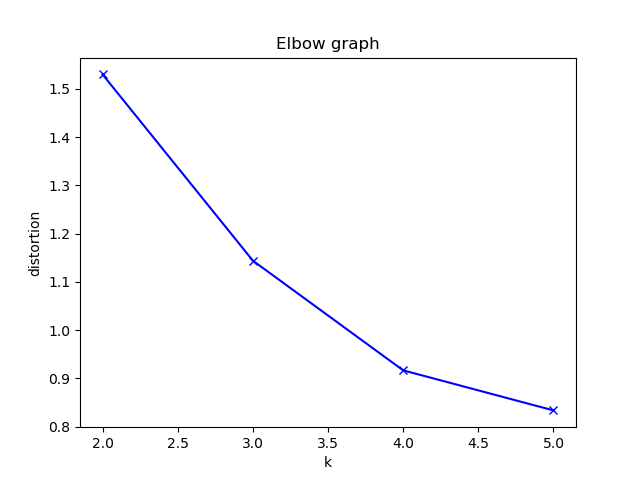
| エルボーグラフ |
今回のエルボーグラフからはK=4が最適と判断しました。
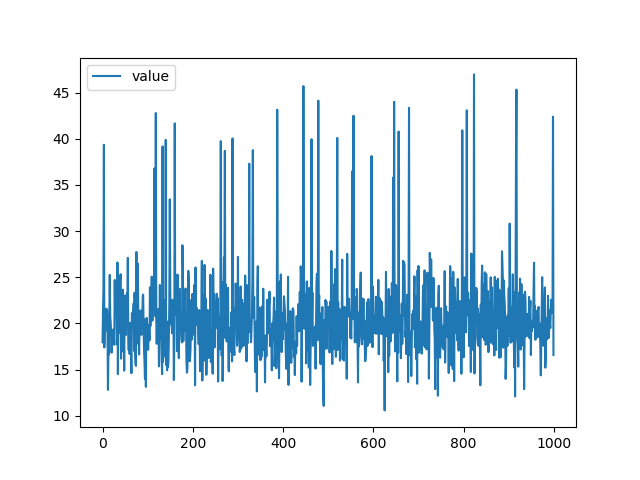
| テストデータ |
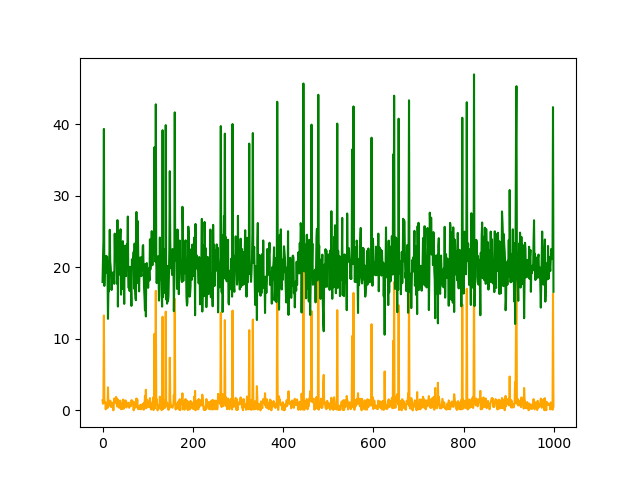
| リザルト |
テストデータも学習データと同じくランダムに値をスパイクさせています。
リザルトグラフはは緑色がテストデータ、黄色が異常スコアですが、データがスパイクしたタイミングで異常スコアも連動して大きく動いていることがわかります。
比例データ
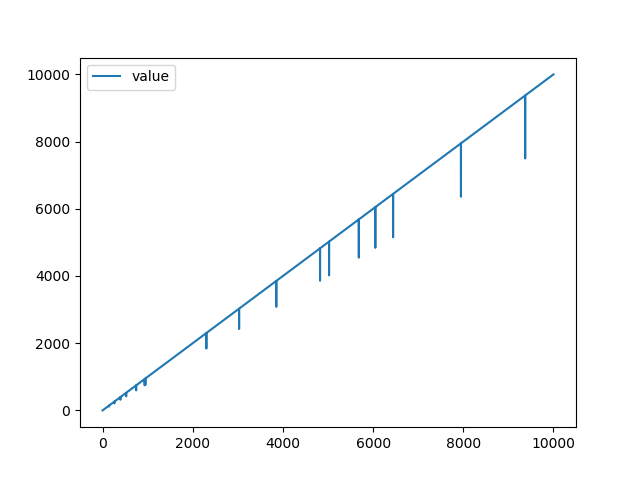
| 学習データ |
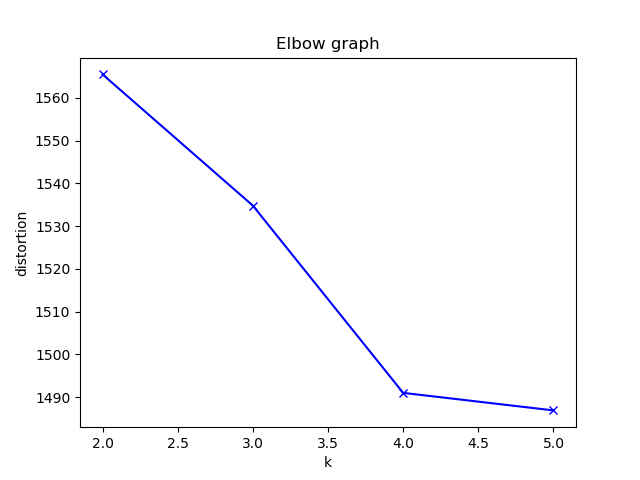
| エルボーグラフ |
今回のエルボーグラフからはK=4が最適と判断しました。
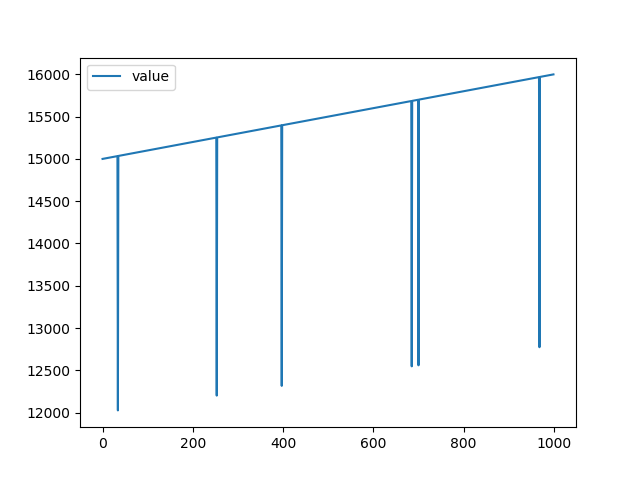
| テストデータ |
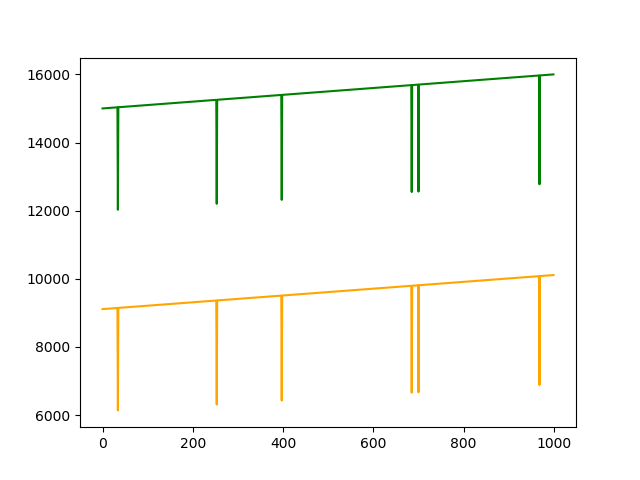
| リザルト |
テストデータは傾きが異なりますが、値の大きさは学習データがそのまま継続していった場合をイメージしています。
リザルトを見てみるとおそらく値の大きさがが学習データから増えていることが原因で、値が小さいほど異常スコアが低く、正常なデータの方が異常スコアが高いという結果になってしまいました。
周期データ
一般的なsin曲線にノイズとスパイクを追加したものを学習データとして使用しました。
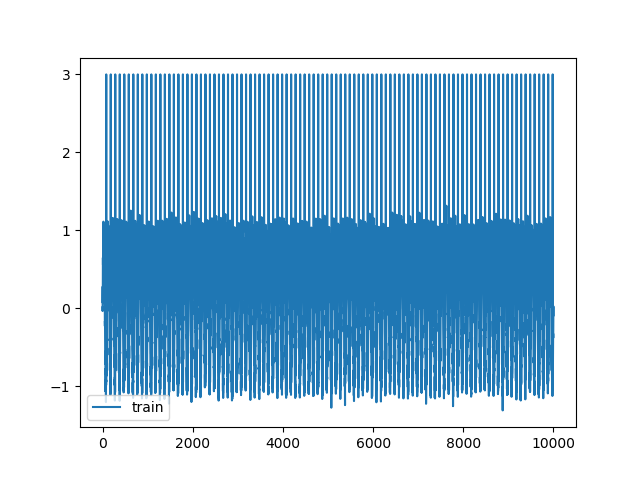
| 学習データ |
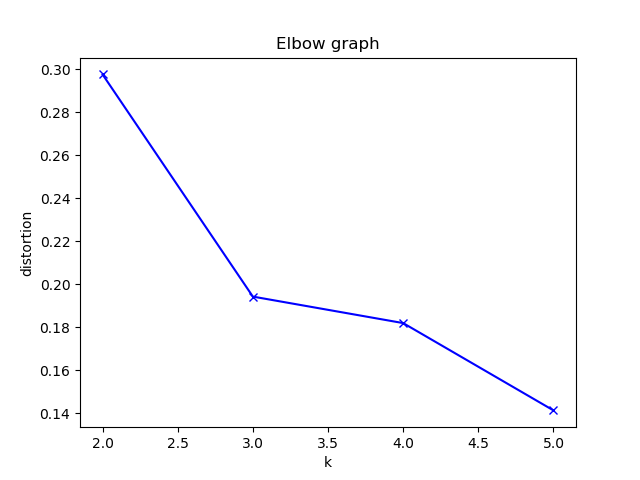
| エルボーグラフ |
今回のエルボーグラフからはK=3が最適と判断しました。
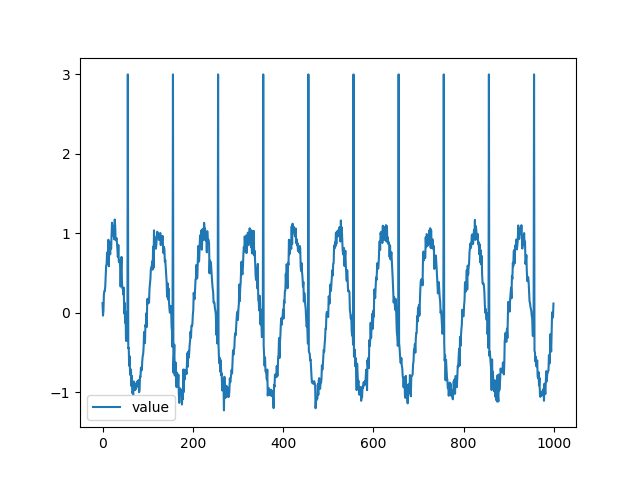
| テストデータ |
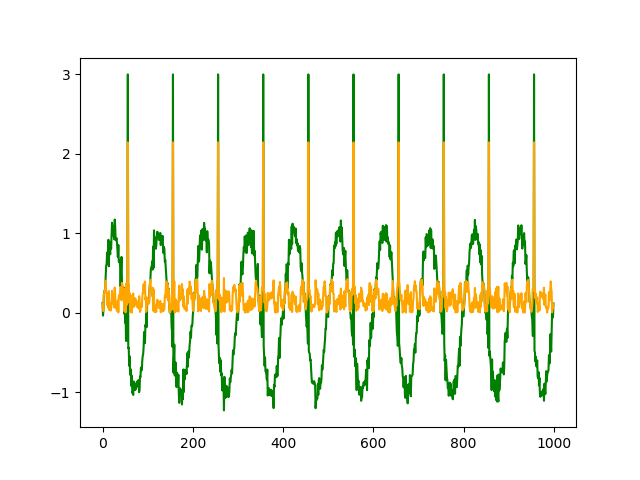
| リザルト |
大きくスパイクするような異常は正確に検知できていることがわかります。
このデータを用いてshingling処理の検証を実施予定でしたが、その前に実際の温度データが手に入ったので以下で落ちらを使用して検証していきます。
実際の温度データ
ここからは私が実際に業務の中で見るような実際の温度データを使用して検証を行っていきます。
このデータの異常検知がしたい。というところから今回の検証は始まっています。
前処理としてshingling処理を行っています。
まずは教師なし(異常データを含むデータで学習)で学習
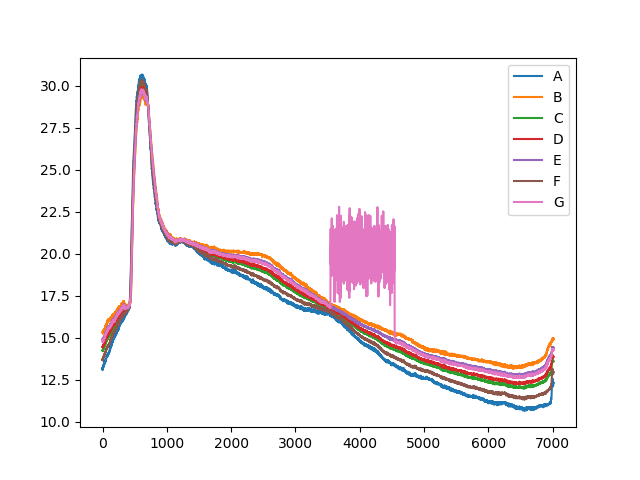
| 学習データ |
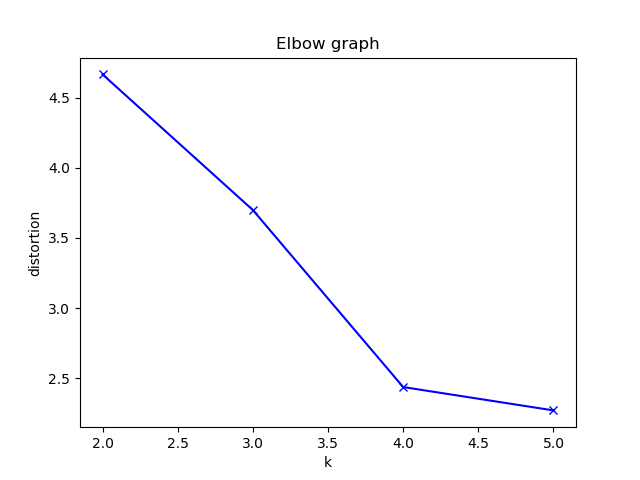
| エルボーグラフ |
今回のエルボーグラフからはK=4が最適と判断しました。
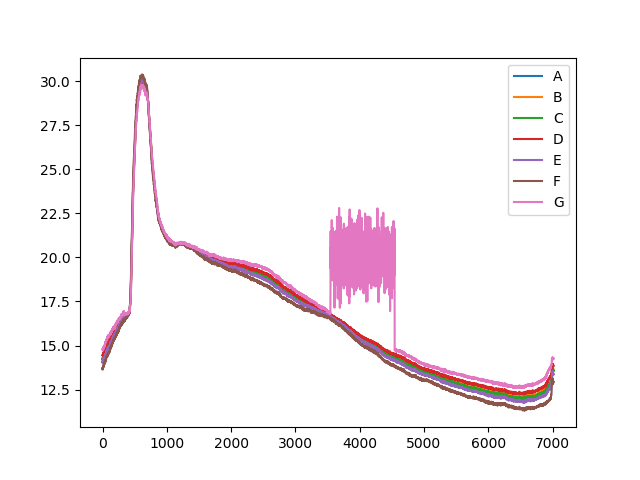
| テストデータ |
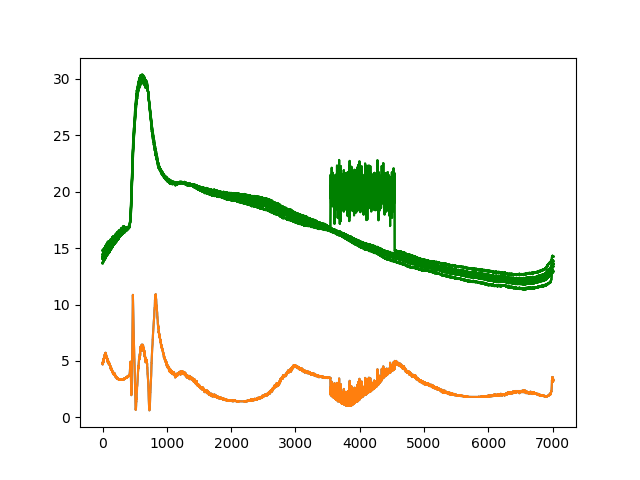
| リザルト |
ダメダメだ。。。
異常と想定した部分のスコアがむしろ下がっています。
教師あり(正常データのみで学習)を試してみる
今度は学習データにスパイクが入っていないものを使用して学習させてみます。
先ほどと同じように前処理としてshingling処理を行っています。
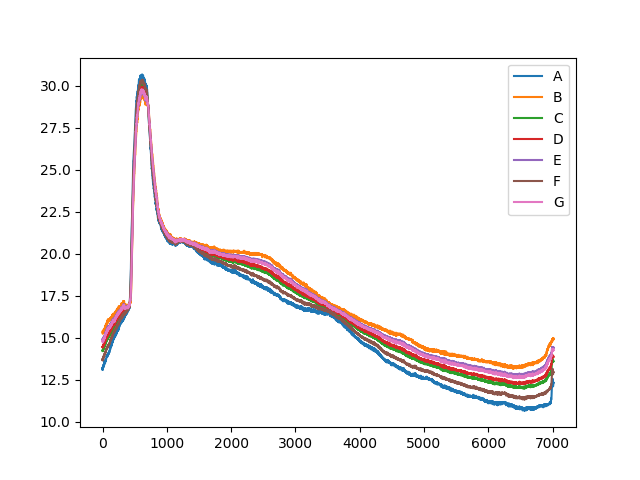
| 学習データ |
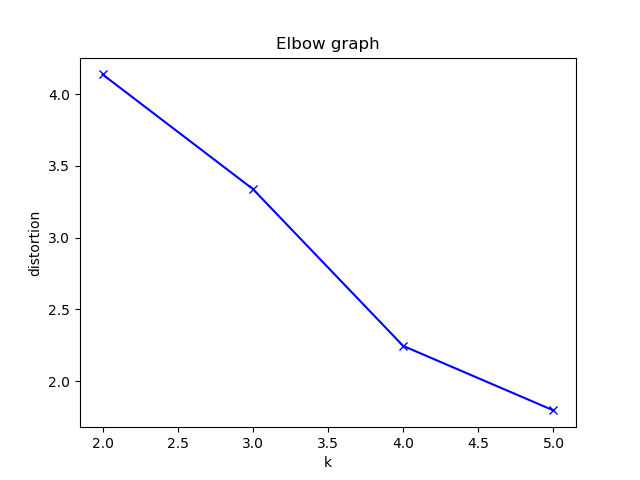
| エルボーグラフ |
今回のエルボーグラフからはK=4が最適と判断しました。
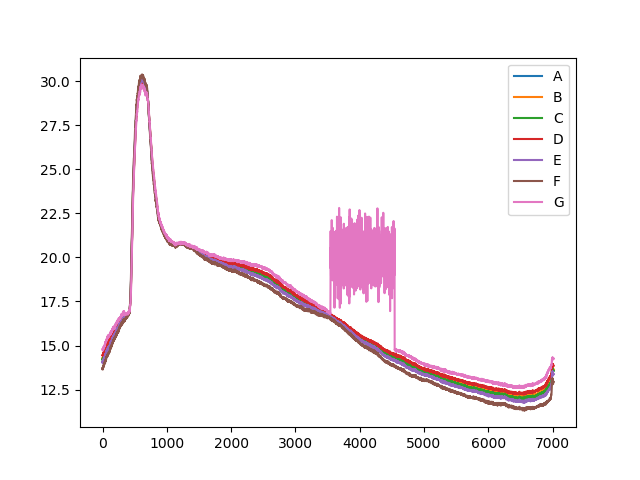
| テストデータ |
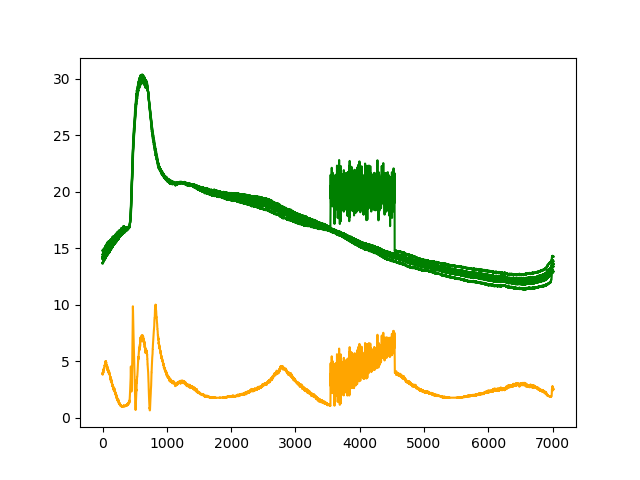
| リザルト |
異常部分でスコアが下がることはなくなったが、値がそもそも大きく逸脱していない異常(通常時とは異なっている程度)は検知が難しい。
うまくいかなかったのでリザルトグラフのどの部分がどのクラスタに属しているのかKを変更して検証してみた
先ほどの検証ではどの部分のデータがどうクラスタリングされた結果異常スコアが出されているのかが分かりづらかったため、クラスターごとに色を変えてリザルトをプロットしてみました。
またクラスタ数の変化でデータの切り分け方がどう変わるのかを確かめるためKを2~5の間で変化させそれぞれ検証を実施しました。
検証は引き続き教師ありの状態で行っています。
K=2
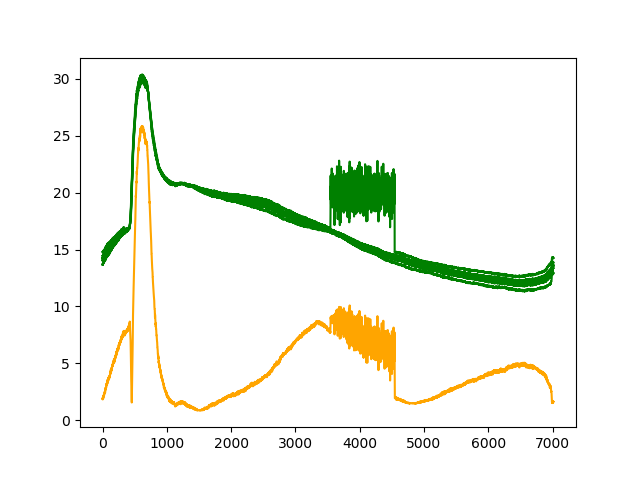
| リザルト |
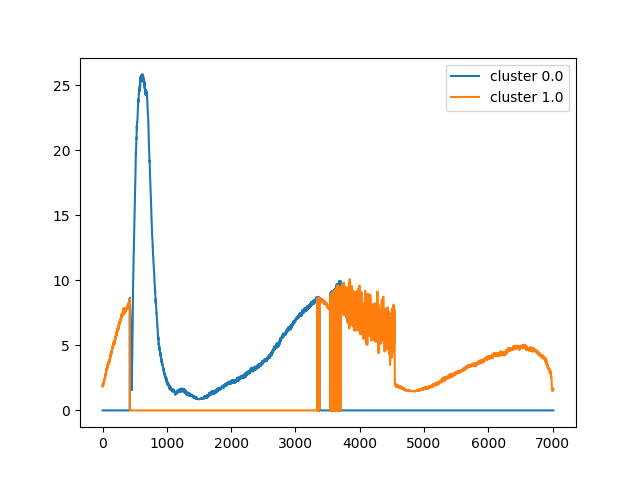
| セグメンテーション |
K=3
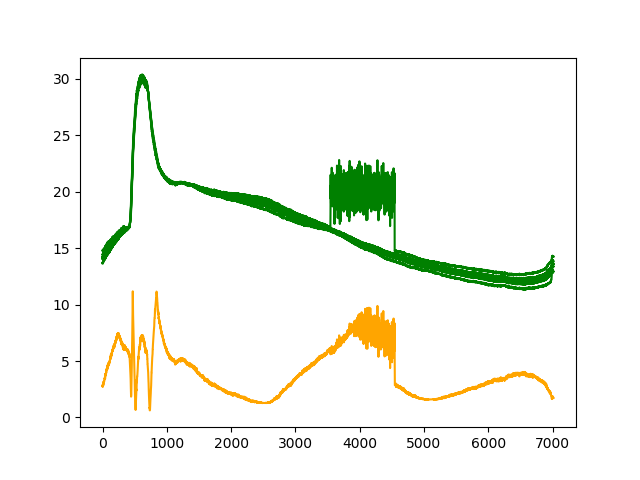
| リザルト |
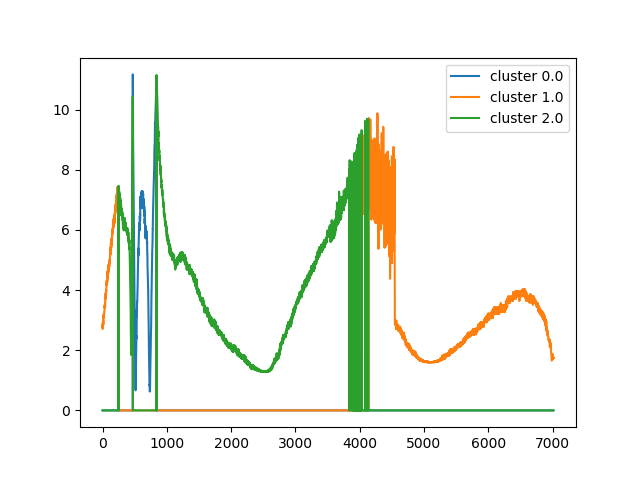
| セグメンテーション |
K=4
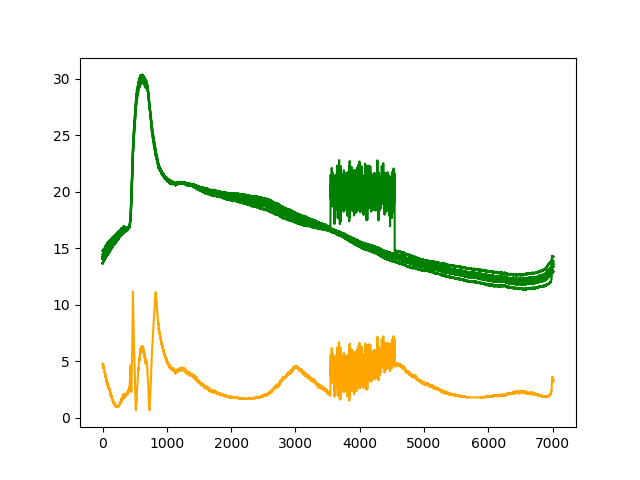
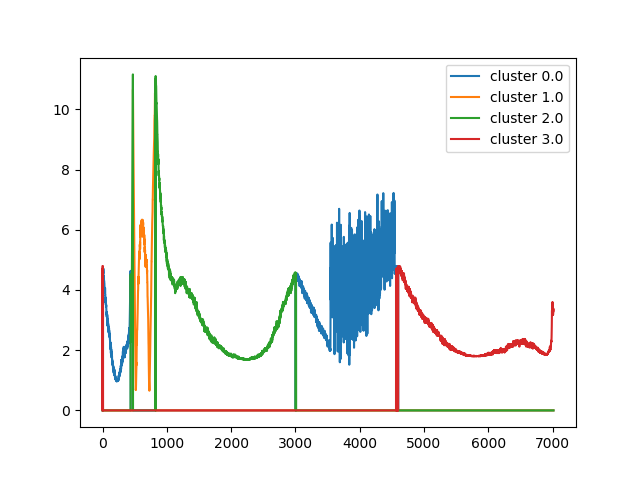
| リザルト |
| セグメンテーション |
K=5
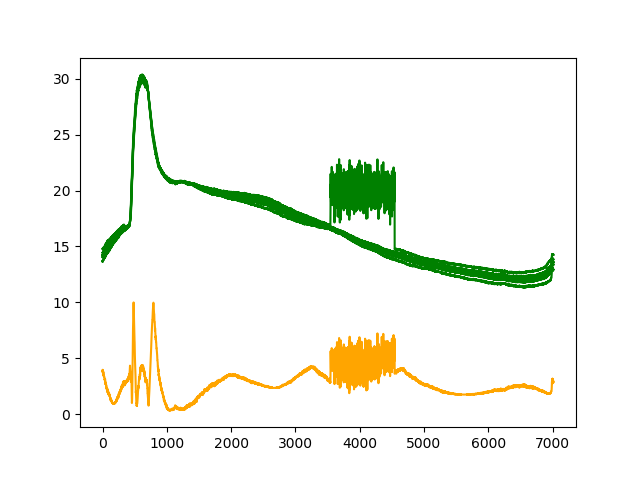
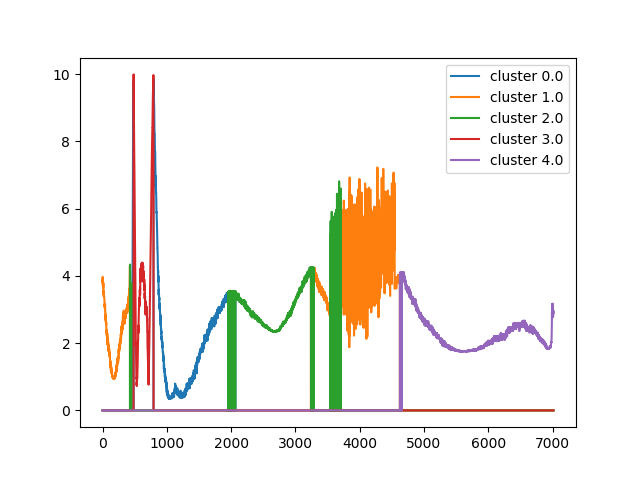
| リザルト |
| セグメンテーション |
なんでうまくいかなかったかをKの値を変えて原因を探ってみました。
そもそもクラスターの中心からの距離で判定するという特性上、一定範囲内の値からスパイクしたものであれば良いですが、今回のような周期データの異常を判定することは難しいです。
今回で言うとKの値を2から3へ変更した時におそらく左側の山なり部分に近い場所にクラスターが作成され、異常スコアが下がり想定したものへ近づきはしましたが、それ以降の変化では大きな改善は見られませんでした。
教師ありでの学習の場合、学習データから算出したスコアとテストデータから算出したスコアを比較することで異常を検出することが可能かもしれません。まだまだ検証の余地はありそうです。
まとめ
今回はK-measns法を用いた数値データの異常検知をAmazon Sagemakerのビルドインアルゴリズムを使用して実施してみました。
特徴として容易に実装でき、モデルサイズも小さいため機械学習初学者の私でも比較的簡単に検証することができました。
ただ、良くも悪くも設定するクラスタ数(K)に大きく結果が影響されてしまうので実際のデータの分析を行う場合は最適な結果を得るために試行錯誤が必要そうです。
今回はスコアとしてAmazon Sagemakerのビルドインアルゴリズムで返されるものを直接使って判定しましたが、ここも工夫次第で精度を高めていくことができそうなので今後の課題として色々試してみたいと思います。